ความเข้าใจเกี่ยวกับจํานวนเฉพาะ 1-100 ระหว่าง

จํานวนเฉพาะ 1-100 ป็นจำนวนที่มากกว่า 1 ที่ไม่สามารถหารอย่างลงตัวได้นอกจาก 1 และตัวมันเองเท่านั้น เหล่านี้คือพื้นฐานที่สำคัญของคณิตศาสตร์เพราะมีบทบาทในการเข้ารหัสลับ, คอมพิวเตอร์ และหลายสาขาอื่นๆ การเข้าใจจำนวนเฉพาะจะช่วยให้เรามีความเข้าใจที่ดีขึ้นเกี่ยวกับโครงสร้างและลักษณะทางคณิตศาสตร์อื่นๆ

ในชีวิตประจำวัน, จำนวนเฉพาะถูกใช้ในเทคโนโลยีต่างๆ เช่น การเข้ารหัสข้อมูลที่สำคัญ โดยการศึกษาจำนวนเฉพาะระหว่าง 1 ถึง 100, เราสามารถเริ่มต้นเข้าใจว่าพวกมันมีอิทธิพลต่อคณิตศาสตร์และวิทยาศาสตร์อย่างไร

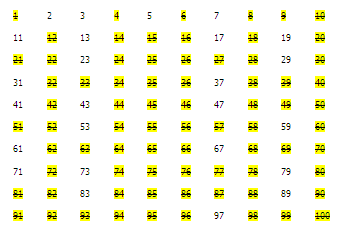
การระบุจำนวนเฉพาะระหว่าง 1 ถึง 100

การระบุจำนวนเฉพาะระหว่าง 1 ถึง 100 เป็นขั้นตอนแรกในการศึกษาคุณสมบัติของพวกมัน จำนวนเฉพาะในช่วงนี้รวมถึง 2, 3, 5, 7, 11, 13, และต่อไปจนถึง 97 ซึ่งเป็นจำนวนเฉพาะที่ใหญ่ที่สุดต่ำกว่า 100 การทำความเข้าใจว่าจำนวนเฉพาะเหล่านี้กระจายอย่างไรช่วยให้เราสามารถคาดการณ์และใช้คุณสมบัติของพวกมันในสูตรและแอปพลิเคชันต่างๆ

ชุดของจำนวนเฉพาะเหล่านี้ยังแสดงให้เห็นถึงความพิเศษที่มีต่อพื้นฐานทางคณิตศาสตร์ พวกมันเป็น “อิฐ” ที่สร้างขึ้นสำหรับตัวเลขทั้งหมด ทุกจำนวนที่ไม่ใช่จำนวนเฉพาะสามารถแยกออกเป็นผลคูณของจำนวนเฉพาะได้ ซึ่งทำให้เราเข้าใจโครงสร้างภายในของตัวเลขที่ซับซ้อนกว่าได้ดีขึ้น.

หลักพื้นฐานของจำนวนเฉพาะ

จํานวนเฉพาะ 1-100มีความสำคัญเพราะพวกมันเป็นพื้นฐานในการหารตัวเลขอื่นๆ โดยไม่มีตัวหารอื่นนอกจาก 1 และตัวเลขนั้นเอง ความหมายนี้ทำให้พวกเขามีบทบาทสำคัญในคณิตศาสตร์ที่สูงขึ้น เช่น การวิเคราะห์ตัวเลขและทฤษฎีเลขคณิต ทำให้เป็นเรื่องง่ายในการแยกตัวประกอบและหาตัวหารที่เป็นไปได้สำหรับตัวเลขที่ใหญ่กว่า

หากจำนวนเฉพาะถูกนำไปใช้ในการคำนวณหรือตั้งสมการ, การเข้าใจคุณสมบัติของจำนวนเฉพาะจะช่วยให้แก้ปัญหาได้ง่ายขึ้น ตัวอย่างเช่น, ในการเข้ารหัสลับ, จำนวนเฉพาะใช้เพื่อสร้างกุญแจที่มีความปลอดภัยสูงเพื่อการเข้ารหัสข้อมูลที่สำคัญ.

บริบททางประวัติศาสตร์ของจำนวนเฉพาะ

การศึกษาเกี่ยวกับจำนวนเฉพาะได้เริ่มขึ้นตั้งแต่สมัยโบราณ นักคณิตศาสตร์กรีกโบราณเช่น ยูคลิด ได้ศึกษาจำนวนเฉพาะและพิสูจน์ได้ว่ามีจำนวนเฉพาะอย่างไม่มีที่สิ้นสุด การศึกษาของเขาเป็นพื้นฐานสำคัญในคณิตศาสตร์และได้รับการพัฒนาต่อยอดโดยนักคณิตศาสตร์ในยุคต่อๆ มา

ตัวอย่างเช่น, ในสมัยของยุคกลางและยุคฟื้นฟูศิลปวิทยา, การศึกษาเกี่ยวกับจำนวนเฉพาะได้ช่วยเหลือในการพัฒนาทฤษฎีตัวเลขและการวิเคราะห์ที่ซับซ้อนยิ่งขึ้น พวกมันยังคงเป็นหัวข้อสำคัญในการวิจัยคณิตศาสตร์ในปัจจุบัน.

จำนวนเฉพาะในคณิตศาสตร์สมัยใหม่

จำนวนเฉพาะมีความสำคัญในคณิตศาสตร์สมัยใหม่และมีการใช้งานในหลายสาขาวิชา เช่น คอมพิวเตอร์ไซเอนซ์, การเข้ารหัสลับ, และวิทยาศาสตร์ข้อมูล ในการเข้ารหัสลับ, จำนวนเฉพาะช่วยในการสร้างระบบที่ปลอดภัยสำหรับการสื่อสารและการเก็บรักษาข้อมูลที่ละเอียดอ่อน จำนวนเฉพาะยังมีบทบาทในอัลกอริทึมต่างๆ ที่ใช้ในการคำนวณและการแก้ไขปัญหาทางคณิตศาสตร์ที่ซับซ้อน

ตัวอย่างเช่น, ระบบ RSA ซึ่งเป็นหนึ่งในระบบการเข้ารหัสข้อมูลที่นิยมใช้กันมากที่สุด, ใช้จำนวนเฉพาะสองจำนวนที่ใหญ่มากในการสร้างกุญแจ การเลือกจำนวนเฉพาะที่เหมาะสมสามารถเพิ่มความปลอดภัยของข้อมูลที่ถูกเข้ารหัส

การสร้างภาพจำนวนเฉพาะ: รูปแบบและการแจกแจง

การมองเห็นลักษณะและการกระจายของจำนวนเฉพาะสามารถให้ความเข้าใจที่ลึกซึ้งยิ่งขึ้นเกี่ยวกับพวกมัน จำนวนเฉพาะมีการกระจายตัวอย่างเฉพาะเจาะจงในช่วงตัวเลขที่กว้างขึ้น, และการวิเคราะห์การกระจายตัวนี้สามารถช่วยในการทำนายและคาดการณ์พฤติกรรมของจำนวนเฉพาะในช่วงต่างๆ

ผู้ที่ศึกษาคณิตศาสตร์อาจสังเกตเห็นว่าจำนวนเฉพาะดูเหมือนจะหายากขึ้นเมื่อตัวเลขมีขนาดใหญ่ขึ้น การกระจายนี้ไม่ได้สม่ำเสมอแต่มีแนวโน้มที่จะตามรูปแบบทางสถิติที่สามารถเป็นที่น่าสนใจ

เทคนิคการระบุจำนวนเฉพาะ

วิธีการหาจำนวนเฉพาะมีหลายวิธี ตัวอย่างเช่น, กระบวนการ Sieve of Eratosthenes เป็นหนึ่งในวิธีโบราณและได้ผลดีที่สุดในการกรองจำนวนเฉพาะจากชุดตัวเลขที่กำหนด วิธีนี้เริ่มต้นด้วยการกำหนดจำนวนเฉพาะที่รู้จักแล้วและใช้พวกเขาเพื่อกำจัดจำนวนที่เป็นไปได้ซึ่งไม่ใช่จำนวนเฉพาะ

การใช้อัลกอริทึมขั้นสูงอื่นๆ เช่น การทดสอบ Miller-Rabin หรือการทดสอบ Fermat ยังสามารถใช้ในการระบุจำนวนเฉพาะได้ วิธีเหล่านี้มีประสิทธิภาพในการจัดการกับตัวเลขขนาดใหญ่และใช้ในระบบคอมพิวเตอร์สมัยใหม่

บทบาทของจำนวนเฉพาะในคณิตศาสตร์ขั้นสูง

จำนวนเฉพาะมีบทบาทสำคัญในคณิตศาสตร์ขั้นสูง พวกเขาช่วยในการศึกษาและการพัฒนาทฤษฎีตัวเลขซึ่งเป็นสาขาวิชาที่สำคัญในคณิตศาสตร์ จำนวนเฉพาะเป็นส่วนสำคัญในการค้นคว้าและการพัฒนาทฤษฎีเกี่ยวกับตัวเลขและการกระจายของพวกมัน(การสำรวจลึกถึงเพลง “เนื้อเพลงโดย ชนกันต์ รัตนอุดม อ้าว: เนื้อหา, ความหมาย, และอื่นๆ)

พวกมันยังมีบทบาทในการพัฒนาและการทดสอบอัลกอริทึมที่ใช้ในคอมพิวเตอร์และฟิสิกส์ การเข้าใจจำนวนเฉพาะและคุณสมบัติของพวกมันช่วยให้นักวิทยาศาสตร์และนักคณิตศาสตร์สามารถแก้ปัญหาที่ซับซ้อนและท้าทายได้

บทสรุป: ความลึกลับที่คงอยู่ของจำนวนเฉพาะ

จำนวนเฉพาะยังคงเป็นหัวข้อที่น่าสนใจและท้าทายในคณิตศาสตร์ พวกมันไม่เพียงแต่เป็นพื้นฐานของหลายสูตรและการคำนวณแต่ยังเป็นส่วนสำคัญในการพัฒนาทฤษฎีใหม่ๆ และการค้นพบในวิทยาศาสตร์ การศึกษาจำนวนเฉพาะช่วยเปิดเผยความลับของธรรมชาติและความสัมพันธ์ที่ซ่อนอยู่ในโลกของตัวเลข